Chapter Overview
Fractions and decimals are essential parts of everyday life. Whether you are dividing a pizza or dealing with money, you are using fractions or decimals. This chapter helps Class 7 students understand how to work with these numbers in a simple and effective way.
Click On The Name To Go To A Specific Topic:
What is a Fraction?
A fraction represents a part of a whole.
Standard Form:
Types of Fractions:
1. Proper Fractions
- A proper fraction has the numerator less than the denominator.
- It represents a value less than 1.
Examples:
3/4, 5/9, 7/8 etc.
Tip: The top number (numerator) is smaller than the bottom number.
2. Improper Fractions
- An improper fraction has the numerator greater than or equal to the denominator.
- It represents a value equal to or greater than 1.
Examples:
4/3, 5/2, 7/5 etc.
Tip: Numerator is greater than or equal to the denominator.
3. Mixed Fractions (Mixed Numbers)
- A mixed fraction combines a whole number and a proper fraction.
- It is just another way of writing an improper fraction.
Examples:
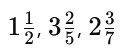
Conversion:
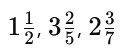
Solutions:
(2×1+1)/2 = 3/2, (5×3+2)/5 = 17/5, (7×2+3)/7 = 17/7
4. Like Fractions
- Fractions that have the same denominator are called like fractions.
Examples:
4/7, 5/7, 3/7 etc.
Note: Like fractions are easy to add or subtract.
5. Unlike Fractions
- Fractions that have different denominators are called unlike fractions.
Examples:
4/7, 5/8, 3/5 etc.
Note: Unlike fractions must be converted to like fractions before performing operations.
6. Equivalent Fractions
- Fractions that represent the same value but look different are called equivalent fractions.
Examples:
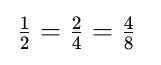
Method: Multiply or divide both numerator and denominator by the same number.
In Short:
- Proper Fraction – Numerator < Denominator (e.g., 3/4)
- Improper Fraction – Numerator ≥ Denominator (e.g., 7/4)
- Mixed Fraction – A whole number with a fraction (e.g., 1⅓)
- Like Fractions – Same denominators (e.g., 2/7, 4/7)
- Unlike Fractions – Different denominators (e.g., 1/2, 2/3)
Bonus: Visual Tip
| Type | Example | Value |
|---|---|---|
| Proper | 3/5 | < 1 |
| Improper | 7/4 | > 1 |
| Mixed | 1¾ | > 1 |
| Like | 1/6, 5/6 | Same Denominator |
| Unlike | 1/2, 2/3 | Different Denominator |
| Equivalent | 2/4 = 1/2 | Same Value |
Real-Life Example
Imagine a pizza cut into 4 equal parts:
If you eat 1 slice = 1/4 → Proper fraction
If you eat all 4 = 4/4 = 1 → Improper fraction
If you eat 5 slices (from another pizza too!) = 5/4 = 1 (1/4) → Mixed fractionOperations on Fractions
1. Addition or Subtraction of Fractions
- Like Fractions: Add or subtract numerators, keep the denominator same.
- Unlike Fractions: Convert to like fractions using LCM, then proceed.
Example:
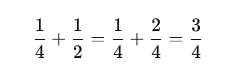
2. Multiplication of Fractions
Multiply numerators and denominators directly.
Example:
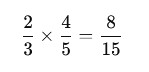
3. Division of Fractions
Multiply by the reciprocal of the second fraction.
Example:
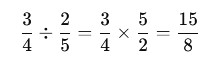
What is a Decimal?
A decimal is another way of representing fractions, especially those with denominators like 10, 100, 1000, etc.
Examples:
0.5 = ½
0.75 = ¾Place Value in Decimals:
| Number | Place Values |
|---|---|
| 45.327 | 4 tens, 5 ones, 3 tenths, 2 hundredths, 7 thousandths |
Operations on Decimals
1. Addition and ➖ Subtraction of Decimals:
- Write numbers one below the other, aligning the decimal point.
- Add/subtract as usual.
2. Multiplication of Decimals:
- Multiply as whole numbers.
- Count total decimal places in both numbers and place the decimal in the answer.
Example:
2.3 × 1.2 = 2.763. Division of Decimals:
- Convert the divisor into a whole number by multiplying by powers of 10.
- Do the same for the dividend and divide.
Example:
3.6 ÷ 0.3 = 36/3 = 12Converting Between Fractions and Decimals
Fraction to Decimal:
Divide numerator by denominator.
3/4 = 0.75Decimal to Fraction:
Write the decimal as a fraction with denominator 10, 100, etc., and simplify.
0.6 = 6/10 = 3/5Important Summary Points
- Convert unlike fractions before adding or subtracting.
- Always align decimal points during addition/subtraction.
- Decimal multiplication requires counting total decimal places.
- Divide decimals by removing the decimal point and adjusting accordingly.
Fun & Educational Facts – Fractions and Decimals
1. Fractions are older than the decimal system!
The concept of fractions was used by ancient Egyptians over 4000 years ago, while the decimal system became popular much later through the work of Indian mathematician Aryabhata and Persian scholars.
2. Decimals are just another way to write fractions.
For example, 0.5 and ½ mean the same thing — they just look different!
3. Repeating decimals are fractions in disguise.
Decimals like 0.333… are repeating decimals and can be converted into fractions like ⅓.
4. Fractions and decimals are part of rational numbers.
Any number that can be written as a fraction (p/q form) is a rational number — this includes both positive and negative decimals and fractions.
5. Decimals make money and measurement easier.
When we say ₹9.75, it’s actually 9 rupees and ¾ of a rupee — decimals help us handle money, weight, distance, and more efficiently.
6. Every decimal is not a simple fraction.
Some decimals like π (3.14159…) are non-terminating and non-repeating, which means they can’t be written as a simple fraction. These are called irrational numbers.
7. Multiplying by powers of 10 shifts decimal places.
Example:
2.5 × 10 = 25
2.5 × 100 = 250
This is a shortcut often used in mental maths!
8. Decimal places are infinite… unless they’re rounded or repeating.
In real-life applications, we round decimals to 2 or 3 places, but in theory, they can continue forever (e.g., ⅓ = 0.333…).
Activity (Exercise):
Fractions and Decimals Class 7 Master Notes (www.jngacademy.com)Coming Soon…
Quiz:
Coming Soon…
Supplementary Materials:
Provide downloadable materials for learners to review:
- – PDF Guide: “Coming Soon”
- – Cheat Sheet: “Coming Soon”
- – Video Source: “JNG ACADEMY“
- – Articles: “Blog Page“

FAQs:
Q1. What are fractions and decimals in Class 7 Maths?
Q2. How are fractions and decimals related?
For example, ½ is the same as 0.5. You can convert between them easily by division or multiplication.
Q3. How to convert a fraction into a decimal?
Example:
⅗ = 3 ÷ 5 = 0.6
Q4. How to convert a decimal into a fraction?
Example:
0.75 = 75/100 = ¾
Q5. What are the types of fractions taught in Class 7?
Improper Fractions (numerator ≥ denominator)
Mixed Fractions (a whole number with a fraction)
Like & Unlike Fractions
Q6. What is the easiest way to add or subtract decimals?
Add or subtract like normal numbers
Place the decimal point in the same position in the result
Q7. Where do we use fractions and decimals in real life?
Money (₹2.50)
Measurement (5.5 kg)
Cooking (¾ cup of sugar)
Shopping discounts (25% = 0.25)

Great line up. We will be linking to this great article on our site. Keep up the good writing.
Thank you so much! I really appreciate you linking to the article. It means a lot, and I’ll keep sharing more helpful content—stay tuned!