Key Learning Outcomes
By the end of this lesson, readers will:
✔️ Understand the concept of positive and negative numbers.
✔️ Learn how to represent integers on a number line.
✔️ Perform addition, subtraction, multiplication, and division of integers.
✔️ Understand important properties of integers, such as commutative, associative, and distributive properties.
✔️ Solve real-life problems using integers, such as temperature, elevation, and financial transactions.
Click On The Name To Go To A Specific Topic:
Introduction to Integers
Integers are a set of numbers that include positive numbers, negative numbers, and zero but not fractions or decimals.
- Positive Integers: Numbers greater than zero (1, 2, 3, 4,…).
- Negative Integers: Numbers less than zero (-1, -2, -3, -4,…).
- Zero (0): It is neither positive nor negative but plays a significant role in integer operations.
Representation of Integers on Number Line
Integers can be represented on a horizontal number line, where:
- Positive numbers are on the right of zero.
- Negative numbers are on the left of zero.
- The greater the number, the more right it is on the number line.
Diagram: Integer Number Line
← -5 -4 -3 -2 -1 0 +1 +2 +3 +4 +5 →
Operations on Integers
1. Addition of Integers
Rules for addition:
- Same Sign: Add the absolute values and keep the common sign.
- Example: (-3) + (-5) = -8
- Different Sign: Subtract the absolute values and take the sign of the greater number.
Example: (-7) + (+4) = -3
2. Subtraction of Integers
To subtract an integer, add the additive inverse (change the sign of the second number and then add).
Example: (-5) – (-3) = -5 + 3 = -2
3. Multiplication of Integers
Rules:
- Positive × Positive = Positive → (+3) × (+4) = +12
- Negative × Negative = Positive → (-3) × (-4) = +12
- Positive × Negative = Negative → (+3) × (-4) = -12
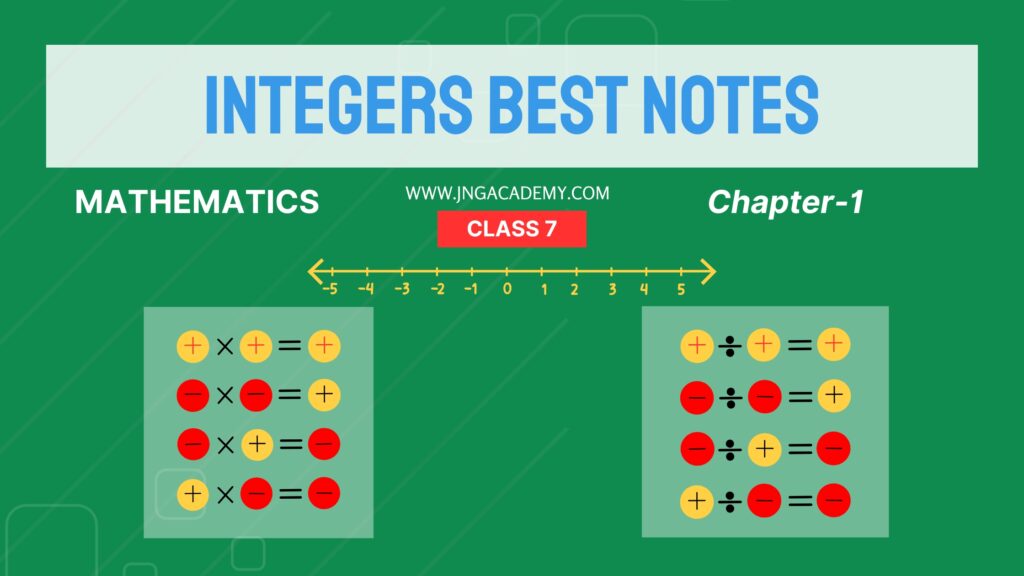
4. Division of Integers
Rules:
- Positive ÷ Positive = Positive → (+12) ÷ (+3) = +4
- Negative ÷ Negative = Positive → (-12) ÷ (-3) = +4
- Positive ÷ Negative = Negative → (+12) ÷ (-3) = -4
Properties of Integers
1. Closure Property
- Addition & Multiplication: Always closed (result is always an integer).
- Subtraction & Division: May not be closed.
2. Commutative Property
- Addition & Multiplication: a + b = b + a, a × b = b × a.
- Subtraction & Division: Not commutative.
3. Associative Property
- Addition & Multiplication: (a + b) + c = a + (b + c).
- Subtraction & Division: Not associative.
4. Distributive Property
- a × (b + c) = (a × b) + (a × c).
Important Summary Points
✔️ Integers include positive numbers, negative numbers, and zero.
✔️ Addition and multiplication of integers follow commutative and associative properties.
✔️ The product of two negative numbers is always positive.
✔️ Subtraction means adding the opposite.
✔️ Integers are useful in daily life for temperature, banking, and elevation measurements.
Interesting Facts About Integers
💡 The word “integer” comes from Latin, meaning “whole.”
💡 In real life, integers are used in thermometers, elevators, bank transactions, and GPS coordinates.
💡 The smallest integer is negative infinity, and the largest integer is positive infinity.
Activity (Exercise):
Fill in the Blanks
- (-9) + (____) = 0.
- The product of two negative integers is always ____.
- (-7) – (-3) = ____.
Short Answer Questions
- Represent -3 to 5 on a number line.
- Find the value of: (-12) + 7 – (-5) × 2.
- Solve: (-25) ÷ (+5) + (-3) × (-4).
Word Problems
- A submarine is 40 meters below sea level. It moves 15 meters deeper, then rises 20 meters. What is its new depth?
- A company gained ₹5000 in January but lost ₹7000 in February. What is the overall profit or loss?
Quiz:
Coming Soon…
Supplementary Materials:
Provide downloadable materials for learners to review:
- – PDF Guide: “Coming Soon”
- – Cheat Sheet: “Coming Soon”
- – Video Source: “JNG ACADEMY“
- – Articles: “Blog Page“

FAQs:
1. What are integers?
2. What is the difference between whole numbers and integers?
Integers: Include 0 and positive numbers with negative numbers (-3, -2, -1, 0, 1, 2, 3, …).
3. What is the smallest and largest integer?
4. Is zero a positive or negative integer?
5. Can the sum of two negative integers be positive?
Example: (-5) + (-3) = -8
6. What happens when a positive and a negative integer are added?
The answer takes the sign of the larger number.
Example: (+8) + (-5) = 3
7. What is the result of multiplying two negative integers?
Example: (-4) × (-3) = 12
8. Why is (-5) × (-3) = 15?
rule of signs:
Negative × Negative = Positive
Negative × Positive = Negative
So, (-5) × (-3) = +15.
9. How do we subtract integers?
Example: (-7) – (+3) = -7 + (-3) = -10
10. Is division of integers commutative?
Example: (-10) ÷ 5 = -2, but 5 ÷ (-10) ≠ -2
11. How are integers used in real life?
✔️ Banking (credits and debits)
✔️ Temperature measurement (positive for above freezing, negative for below)
✔️ Elevation levels (above and below sea level)
12. What is the absolute value of an integer?
Example: |−7| = 7
13. Can integers be decimal numbers?
14. What is the additive inverse of an integer?
Example: The additive inverse of 5 is -5 because 5 + (-5) = 0.
15. What is the distributive property of integers?
a × (b + c) = (a × b) + (a × c)
Example: 2 × (3 + 4) = (2 × 3) + (2 × 4) = 6 + 8 = 14
